
3D Graphics Programming with QuickDraw 3D 1.5.4
Previous | QD3D Book | Overview | Chapter Contents | Next

3D Graphics Programming with QuickDraw 3D 1.5.4
Previous | QD3D Book | Overview | Chapter Contents | Next
QuickDraw 3D provides four basic polyhedral primitives, three-dimensional surfaces composed of polygonal faces that share edges and vertices with other faces. These are the mesh, the trimesh, the trigrid, and the polyhedron. Although you can use each of these primitives to represent the same sorts of shapes, there are important differences in their memory use, ease of definition, flexibility, and other features. This section describes the four polyhedral primitives individually. Then it compares their strengths and weaknesses (in "Comparison of the Polyhedral Primitives" ). See "Using Geometric Objects" for code samples that show how to construct several different polyhedral primitives.
A mesh is a collection of vertices, faces, and edges that represents a topological polyhedron (that is, a solid figure composed of polygonal faces). The polyhedra represented by QuickDraw 3D meshes do not need to be closed, so that the meshes may have boundaries. Figure 5 illustrates a mesh.

A mesh face is a polygonal figure that forms part of the surface of the mesh. QuickDraw 3D does not require mesh faces to be planar, but you can obtain unexpected results when rendering nonplanar mesh faces with a filled style. In addition, a mesh face can contain holes, as shown in Figure 6 .
Figure 6 A mesh face with a hole
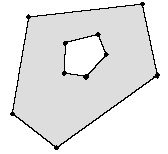
A mesh face is defined by a list of mesh vertices. The ordering of the vertices is unimportant; you can list the vertices of a mesh face in either clockwise or counterclockwise order. QuickDraw 3D internally attempts to maintain a consistent ordering of the vertices of all the faces of a mesh.
Because of their potential complexity, QuickDraw 3D treats meshes differently than it treats all other basic geometric objects. Usually, you create a basic geometric object by filling in a public data structure that completely specifies that object (for example, a structure of type TQ3TriangleData ) and then by passing that structure to the appropriate object-creating routine (for example, Q3Triangle_New ). To create a mesh, however, you first create a new empty mesh (by calling Q3Mesh_New ), and then you explicitly add vertices and faces to the mesh (by calling Q3Mesh_VertexNew and Q3Mesh_FaceNew ).
Although you can manipulate an edge in a mesh (for instance, assign an attribute set to it), you cannot explicitly add an edge to a mesh. Mesh edges are implicitly created or destroyed when the faces containing them are created or destroyed.
Because you can dynamically add or remove faces and vertices in a mesh, a mesh is always a retained object (that is, QuickDraw 3D maintains the mesh data internally) and never an immediate object. As a result, QuickDraw 3D does not supply routines to submit or write meshes in immediate mode. QuickDraw 3D builds an internal data structure that records the topology of a mesh (that is, the edge connections between all the faces and vertices in the mesh). For large models, this might require a large amount of memory. If your application does not need to use the topological information maintained by QuickDraw 3D (which you access by calling mesh iterator functions), you might want to use a trigrid or polyhedron (or a number of triangles, or a number of simple or general polygons) to represent a large number of interconnected polygons.
See "Traversing Mesh Components, Vertices, Faces, and Edges" , for information on the mesh iterator functions.
As you've seen, a face of a mesh can contain one or more holes. A hole is defined by a contour, which is just a list of vertices. You create a contour in a mesh face by creating a face that contains the vertices in the contour (by calling Q3Mesh_FaceNew ) and then by converting the face into a contour (by calling Q3Mesh_FaceToContour ). For optimal results, the face that contains the contour (called the container face ) and the contour itself should be coplanar. In addition, the contour should lie entirely within the container face.
See "Creating a Mesh" for sample code that creates a mesh.
The geometric structure of a mesh is completely defined by its faces, vertices, edges, and contours. For purposes of shading and picking, QuickDraw 3D defines several other parts of a mesh: corners, mesh parts, and components. A mesh corner (or a corner ) is specified by a mesh face together with one of its vertices. (A face with five vertices therefore has five corners.) You can associate a set of attributes with each corner. The attributes in a corner override any existing attributes of the associated vertex. For example, you can use corners to achieve special shading effects, such as hard edges when applying a smooth shading to a mesh. When a face is being shaded smoothly, the normals used to determine the amount of shading are the normals of the face's vertices. Because a vertex and its normal may be associated with several faces, the light intensity computed by a shading algorithm is the same for all points around that vertex. As a result, the edges between appear smooth. To get a hard edge, you can assign different normals to the corners on opposite sides of the edge.
A mesh part object (or, more briefly, a mesh part ) is a single distinguishable part of a mesh. You can use mesh parts to handle user picking in a mesh. When, for example, the user clicks on a mesh, you can interpret the click as a click on the entire mesh, on a face of a mesh, on an edge of the mesh, or on a vertex of the mesh. QuickDraw 3D signals your application that the user clicked on a mesh part by putting a reference to that mesh part in the shapePart field of a hit data structure. (Mesh parts are currently the only types of shape part objects.) You can then call QuickDraw 3D routines to get the mesh face, edge, or vertex that corresponds to the selected mesh part. See the chapter "Pick Objects" for complete details about mesh parts.
A mesh component (or a component ) is a collection of connected vertices. (Two vertices are considered to be connected if an unbroken path of edges exists linking one vertex to the other.) For each mesh, QuickDraw 3D maintains information about the components in the mesh and updates that information whenever a face or vertex is added to or removed from a mesh. You can use QuickDraw 3D routines to iterate through the components in a mesh, and you can call Q3MeshPart_GetComponent to get the component in a mesh that was selected during picking. Mesh components cannot have attributes.
Mesh components are transient; that is, they are created and destroyed dynamically as the topology of the mesh changes. Whenever you change the topology (for example, by adding or deleting a vertex or face), QuickDraw 3D needs to update its internal list of mesh components. You can turn off this updating by calling the Q3Mesh_DelayUpdates function, and you can resume this updating by calling the Q3Mesh_ResumeUpdates function. For performance reasons, it's useful to delay updates while adding or deleting a large number of vertices or faces.
Note, however, that you cannot rely on some mesh functions to return accurate results if you call them while mesh updating is delayed. For instance, the Q3Mesh_GetNumComponents function is not guaranteed to return accurate results if mesh updating is delayed.
Note also that a vertex, edge, or face might be shifted from one component to another during a change in the topology of the mesh. To be safe, you should bracket all changes to the mesh topology by calls to Q3Mesh_DelayUpdates and Q3Mesh_ResumeUpdates , and you should not assume that mesh component functions will return reliable results until after you've called Q3Mesh_ResumeUpdates .
You can duplicate a mesh by calling Q3Object_Duplicate . The duplicate mesh, however, might not preserve the ordering of components, faces, or vertices of the original mesh.
A trigrid is a rectangular grid composed of triangular facets. A trigrid, like most other QuickDraw 3D primitives, is defined using a public data structure, the TQ3TriGridData data type:
typedef struct TQ3TriGridData {
unsigned long numRows;
unsigned long numColumns;
TQ3Vertex3D *vertices;
TQ3AttributeSet *facetAttributeSet;
TQ3AttributeSet triGridAttributeSet;
} TQ3TriGridData;
Once it's defined, a trigrid has a fixed topology defined by the number of rows and columns. You can alter the position of any individual vertex, but you cannot add vertices to (or remove vertices from) a trigrid. In addition, a trigrid can model only rectangular objects, not arbitrary three-dimensional surfaces. Nevertheless, trigrids use memory extremely efficiently and are therefore good choices for modeling rectangular objects.
A polyhedron is a polyhedral primitive, all of whose faces are triangular. (As you'll see below, however, it's possible to render non-triangular faces by selecting which edges of each triangular face are drawn.) The faces of a polyhedron are defined indirectly, using indices into an array of vertices. This indirection makes it easy for faces to share vertices and attribute sets, which thereby reduces both the memory required to define the polyhedron and the time required to render the polyhedron.
The polyhedron is the preferred polyhedral primitive for general-purpose modeling of three-dimensional surfaces. Unlike a trigrid, a polyhedron can represent any surface, not just rectangular ones. In addition, you can use both immediate and retained modes with polyhedra.
To define a polyhedron, you first need to create an array of three-dimensional points (of type TQ3Point3D ). Then you need to define an array of triangles, each of which specifies three of the points in the point array and some additional information about which edges of the triangle to draw and what attributes, if any, the triangle has.
You specify a point in the array of points using a vertex specified by its index into the array of three-dimensional points.
An individual triangular face of a polyhedron is defined by the TQ3PolyhedronTriangleData data type.
typedef struct TQ3PolyhedronTriangleData {
unsigned long vertexIndices[3];
TQ3PolyhedronEdge edgeFlag;
TQ3AttributeSet triangleAttributeSet;
} TQ3PolyhedronTriangleData;
The edgeFlag field specifies which edges of the triangle are to be drawn; see below for more details.
Finally, once you've created the array of points in the array and defined one or more triangular faces for the polyhedron, you can define a polyhedron using the TQ3PolyhedronData data type:
typedef struct TQ3PolyhedronData {
unsigned long numPoints;
TQ3Vertex3D *vertices;
unsigned long numEdges;
TQ3PolyhedronEdgeData *edges;
unsigned long numTriangles;
TQ3PolyhedronTriangleData *triangles;
TQ3AttributeSet polyhedronAttributeSet;
} TQ3PolyhedronData;
This structure specifies the number of points in the polyhedron, the points array, the number of triangles in the polyhedron, and the triangles array. These fields contain the minimum data you need to define a polyhedron.
The polyhedron data structure also contains information about the edges in the polyhedron. You can specify edge information either using the edgeFlag field of each individual triangle, or you can do so using the numEdges and edges fields of the polyhedron data structure. See "Polyhedra" for more information on specifying polyhedron edges.
Trimeshes are similar to polyhedra in that they are defined indirectly, using indices into an array of points. In addition, a trimesh has an optional edge array that defines the edges that are to be drawn. However, trimeshes handle attributes quite differently from all other QuickDraw 3D geometric primitives. You do not store attributes for a trimesh (or for any part of a trimesh) in a set of type TQ3AttributeSet . Instead, you must use a structure of type TQ3TriMeshAttributeData , which stores attribute data contiguously in a single block of memory.
More importantly, attributes associated with a trimesh must conform to this restriction: if any single vertex (or edge, or face) has an attribute of a specific non-custom type, then every vertex (or edge, or face) in the trimesh must also have an attribute of that type. (There are, therefore, no shared attributes.) This restriction can deleteriously affect the memory requirements of a large trimesh.
The trimesh is not suitable for general-purpose use representing polyhedral models. The restrictions on attribute storage can result in very large memory requirements, even though only a few faces might need attributes assigned to them. In addition, there are no functions provided by QuickDraw 3D that allow you to change the geometric or topological configuration of a trimesh object. Trimeshes are designed for immediate mode rendering, and are most suitable for surfaces in which all the component triangles have the same types of attributes.
You can use the four polyhedral primitives--the polyhedron, trimesh, mesh, and trigrid--to create similar shapes. However, these primitives offer important differences in their generality, flexibility, style of programming, performance, and compliance with the overall design goal of treating retained and immediate mode programming as equivalent. Table 3-1 provides an overview of their chracteristics, which are discussed in greater detail in "Using Geometric Objects" .
|
Suitability for general model representation and distribution |
Previous | QD3D Book | Overview | Chapter Contents | Next